
小池文人(島根大学生物資源科学部,生物科学科,現:横浜国立大学環境情報研究院)
相崎守弘(島根大学生物資源科学部,生態環境科学科)
秋葉道宏(島根大学生物資源科学部,生態環境科学科,現:国立公衆衛生院水道工学部)
本庄工区と中海本体とは西部承水路を介して接続している.また潮どおし実験により4月から北部承水路にも連絡した.この報告では,潮どおし実験以前について,本庄工区と中海本体との水の交換の程度を試算した.データは島根大学生物資源科学部環境生態工学科(相崎,秋葉ら)による公開データ(http://vege1.kan.ynu.ac.jp/nakaumi/dataarc/aizaki/aizaki.xls)を使用した.
<方針>
中海本体の塩分濃度は乱高下するが,本庄工区は中海本体の塩分濃度の推移に追随するかたちで変化した.本庄工区と中海本体の水の交換量が多ければ,両者の塩分濃度差はほとんどなくなり,本庄工区は中海本体の塩分濃度変化に敏感に反応する.逆に交換量が少なければ,本庄工区はゆるやかに追随する.
この追随のしかたを調べることによって,水の交換量を逆算できる.これは塩分の収支から水の交換を推定することにあたる.

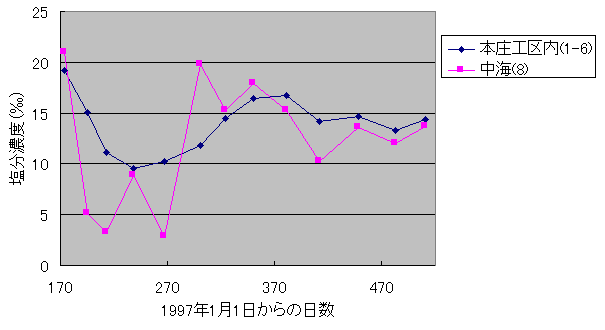
図1.表層水の塩分濃度の推移.調査地点(station)の位置は http://vege1.kan.ynu.ac.jp/nakaumi/dataarc/aizaki/714.html に示されている.Station1からStation6までが本庄工区内であり,Station8は中海本体,Station7は連絡する水路の本庄工区側の開口部にあたる.下の図は本庄工区内の調査地点をすべて平均したもの.島根大学生物資源科学部環境生態工学科(相崎,秋葉ら)による上記の公開データから作成した.
<仮定>
1.本庄工区を中海本体とだけつながる閉鎖水域と考え,本庄工区に直接流れ込む川は無視する
2.本庄工区に降る雨や水面からの蒸発も無視した.ただし塩分濃度が急激に下降するときには本庄工区内への降水も多かったと考えて,この影響を取り除くために本庄工区内の塩分濃度変化が -0.1 (‰/日)より急激に減少している場合は,データを計算から除外した.
3.表層の水だけを考え,本庄工区内で低層水との混合は起きないとした.観測データのうち水深 0-1.0 m の測定値の平均を用いた.本庄工区内は塩分躍層があまり発達しないことが多い(清家,http://vege1.kan.ynu.ac.jp/nakaumi/2/suisitu.htm).また中海との連絡水路は水深が浅いため,中海の表層水のみが本庄工区に出入りする(http://vege1.kan.ynu.ac.jp/nakaumi/dataarc/aizaki/714.html).
4.本庄工区内では表層水は水平方向に良く混ざると仮定した(図1).本庄工区内の6箇所の調査地点の平均値を本庄工区の値とした.
<方法>
記号
H: 本庄工区の塩分濃度
N: 中海の塩分濃度
x: 1日あたり,本庄工区の表層水のどれくらいの割合が入れ替わるか
ある日の塩分濃度が,本庄工区でH,中海でNだったとする.
翌日は本庄工区の水のうちxだけが入れ替わるので,
翌日の本庄工区の塩分濃度 = (1 - x)H + xN
この間の1日間の塩分濃度変化は
本庄工区の塩分濃度変化 = 当日の濃度 − 前日の濃度
= (1 - x)H + xN - H
= x(N - H)
そこで,本庄工区と中海本体の塩分濃度の差(N-H)と,本庄工区の1日あたりの塩分濃度の変化速度のグラフを描けば,回帰直線の傾きが水の入れ替わり率になる.
ただし,通常の最小二乗法では傾きが小さく計算される傾向があるため,
傾き = 縦軸の標準偏差 / 横軸の標準偏差
として計算した (Sokal & Rohlf 1995, BIOMETRY,説明文はこちら).
<結果>
1日に本庄工区の水の2.171%が中海の水と入れ替わっていた(図2).この入れ替わり率では,約1月(31.6日)で半分の水が入れ替わる.95%の水が入れ替わるのには約4.5ヶ月(136日)かかる.
本庄工区の面積と容量は16.23 km2,容量は8248 万トン(82,486,958 m3)で平均水深は5.1mである(相崎未発表).この値を使って2.171%の交換率での交換流量を計算すると
8248*0.02171=179
179万トン/日になる.高安(http://takayasu.soc.shimane-u.ac.jp/Honjo_Koku/honjo_koku_index.htm)が実測した数値にも近い.
この推定の信頼性をブートストラップ法で調べた.本庄工区の入替率の中央値は2.22%で,50%信頼区間をあらわす第1四分位数と第3四分位数はそれぞれ1.93%と2.53%だった.90%信頼区間は1.17%〜3.49%までのあいだである.(プログラムとデータはこちら)
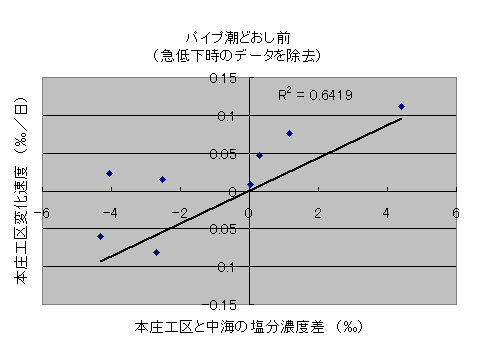
図2.本庄工区と中海本体の塩分濃度差と,本庄工区の塩分濃度の1日あたりの変化量の関係.97年8月1日から98年2月24日までのデータを用いた.本庄工区の塩分濃度が急低下したときには本庄工区内への大量の降雨も考えられるので,そのようなデータは計算からはずした.
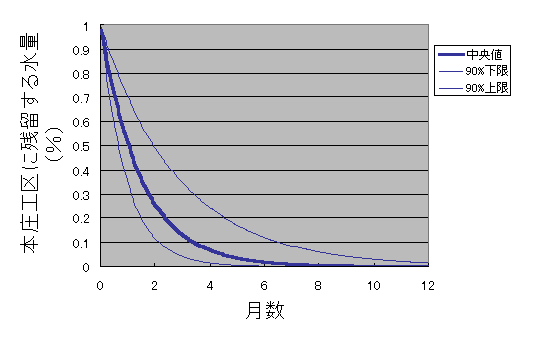
図3.水の交換により,本庄工区に残留する水が減って行くようす.ブートストラップ法の90%信頼限界で,入れ替わり率が高い場合は5ヶ月くらいでほとんどすべての水が入れ替わるが,遅い場合は1年たった後も1.4%程度が残留する.
<もっと精度を上げるには>
1.台風や大雨の日は除いて計算する.
2.夏と冬では水位が違うので,交換率も違うかもしれない.
3.その他に,川から流入する水量や蒸発量を含めて水と塩分の収支をきっちり計算しても良いかも知れないが,相当大変な観測と計算が必要になる.
<おわりに>
1.今回は通水前のデータのみだが,パイプによる通水後の入れ替わり率の値の変化も知る必要がある.
2.計算には公開データを使用したが,さまざまなひとがさまざまな角度から結果を解析するには,データの公開はとても有効だと思われる.
3.北陸先端科学技術大学院大学の上野博芳氏にはこの報告を読んでアドバイスをいただきました.感謝します.
4.今回の計算は大まかな試算ですが「そんな計算ではいけない」とか「他の人が計算している」というような意見や情報などがありましたらお寄せください.
新しい通水パイプからの水の交換を加えたモデルは以下のようになる.
記号
H: 本庄工区の塩分濃度
N: 中海の塩分濃度
P: 北部承水路(貯木場)の塩分濃度
x: 西部承水路から,本庄工区の表層水のどれくらいの割合が1日で入れ替わるか
y: 通水パイプから,本庄工区の表層水のどれくらいの割合が1日で入れ替わるか
ある日の塩分濃度が,本庄工区でH,中海でN,北部の貯木場でPだったとする.
翌日は本庄工区の水のうちx+yだけが入れ替わるので,
翌日の本庄工区の塩分濃度 = (1 - x - y)H + xN + yP
この間の1日間の塩分濃度変化は
本庄工区の塩分濃度変化 = 当日の濃度 − 前日の濃度
= (1 - x - y)H + xN + yP - H
= x(N - H) + y(P - H)
そこで,本庄工区と中海本体の塩分濃度の差(N-H)と,本庄工区と北部の貯木場の塩分濃度差(P-H),さらに本庄工区の1日あたりの塩分濃度の変化速度との間の3次元空間での回帰平面を求めれば,そのパラメータがそれぞれの水路を通っての入れ替わり率になる.
しかし,中海本体と貯木場の塩分濃度差が独立に変動してくれれば良いのだが,実際には極めて近い値をとっている.その場合は以前と同じ解析を行うことになる.通水パイプ設置による交換率全体の変化はわかるが,残念ながらどちらの水路がどれだけ貢献しているのかを分離して評価することはできなくなる.
連絡先:小池(koikef@ynu.ac.jp)