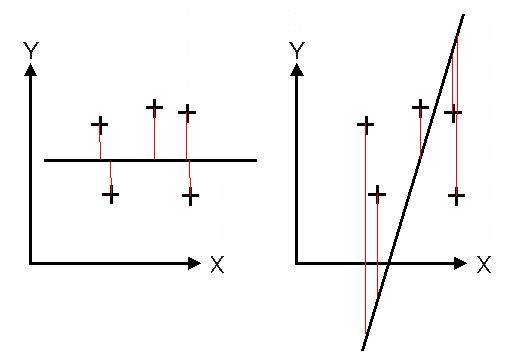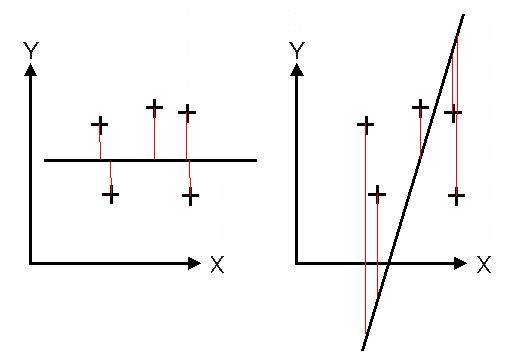最小二乗法を使わない簡単な直線回帰のやりかた
(reduced major axis)
xとyの2つの変数の関係の近似式を求めるときには,最小二乗法を使うことが多い.
しかし,より簡単で望ましい性質を持った方法もある(Sokal & Rholf, BIOMETRY).
<簡単で便利な方法>
1.横軸xと縦軸yのグラフを描く
2.xとyのそれぞれの平均値と標準偏差を計算する.
3.xとyを正規化する
x’=(x−xの平均)/xの標準偏差
y’=(y−yの平均)/yの標準偏差
4.x’とy’とでグラフを描く
5.このグラフが右上がりなら,原点をとおって右上がり45度の直線を描く.この線のまわりにデータのプロットがあるはずで,これが回帰直線になっている.この式は
y’=x’
(y−yの平均)/yの標準偏差=(x−xの平均)/xの標準偏差
y=(y標準偏差/x標準偏差)x + y平均 − x平均 * y標準偏差/x標準偏差
グラフが右下がりなら,原点をとおって右上がり45度の直線を描く.この式は
y’= −x’
になる.
6.もとのxとyのグラフの上では,この直線は点(x平均,y平均)をとおり傾きがy標準偏差/x標準偏差の直線になる.ただし右下がりのグラフの場合は,同じく点(x平均,y平均)をとおり,傾きがy標準偏差/x標準偏差の直線になる.
7.右下がりか右上がりか迷ったときには,4番の正規化したデータについて,それぞれのデータ点でx’* y’の掛け算をおこなう.この値を全部のデータ点で平均すると相関係数が得られる(厳密にはこの平均値を計算するときにデータ個数でなくデータ個数-1で割り算してある補正を行う).これがプラスなら右上がり,マイナスなら右下がりとする.数表などで検定して相関係数が有意でなければ線を引かない.
<この方法の利点>
1.直線回帰には,この方法と,主成分分析のプログラム,さらに普通の最小二乗回帰が使われる.特に最小二乗回帰が多い.
2.しかし,この方法は原理が簡単なので中学生でも理解して計算できる.最小二乗法の理解には微分が必要.
3.直線の傾きの推定値が,最小二乗法ではより小さい方向にずれることが知られている.回帰直線の傾きの値を重要なパラメータとして使用したい場合には,最小二乗法は良くない.
4.得られる結果は主成分分析を使った近似直線と同じだが,主成分分析のプログラムを使うよりも簡単である.
<なぜ最小二乗法では傾きの推定値がずれるのか>
1.最小二乗法では,データ点から直線まで,縦におろした線の長さの2乗を計算し,これの全部のデータ点での値の合計を計算して,これがもっとも小さくなるように直線を決めている(図1).xの値からyの値を推定するため方法なので,測定機器の検量線を引くには良い方法である.

2.もしxとyに全く相関がない場合には,回帰直線は横に引いても縦に引いても変わらないはずである(図2).ところが,実際には直線の傾きを急にすると直線との縦方向の距離が大きなデータ点が出現してしまうため,無相関のときには水平な回帰直線が得られる.
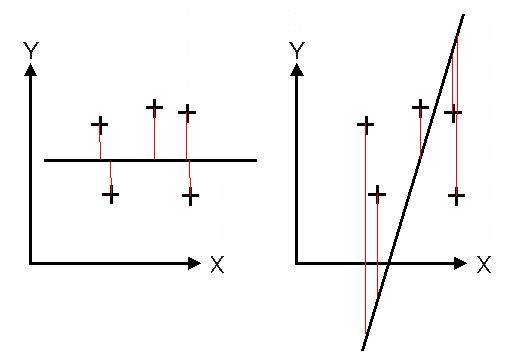
3.同様に,相関が弱いときには回帰直線の傾きは真の値より小さめに出てしまう.
<参考文献>
Sokal,R.R. & Rholf, F.J., 1995. Biometry. 3rd edition. Freeman.
粕谷英一 1998 生物学を学ぶ人のための統計のはなし −君にも出せる有意差−.文一総合出版.
小池文人
〒240-8501 横浜市保土ヶ谷区常盤台79-7
横浜国立大学環境情報研究院
電話・Fax 045-339-4356 koikef@ynu.ac.jp
http://vege1.kan.ynu.ac.jp