過去のページです

現在のページはこちら

新型コロナウイルス感染症COVID-19

英名：　Novel Coronavirus Disease 2019

病原体：　SARS-CoV-2

原産地・生態： ヒトの感染症．2019年末に中国武漢市周辺から分布拡大．野生脊椎動物に感染するウイルスがヒトへの感染能力を獲得したと考えられている．

情報源

厚生労働省:　 新型コロナウイルス感染症についてhttps://www.mhlw.go.jp/stf/seisakunitsuite/bunya/0000164708_00001.html

2021年9月28日時点

将来予測

これらの予測はひとつの方法によるものであって誤差を含み，今後の感染拡大防止策などにより変化すると考えられる．また季節性や人工的な免疫は考慮されていない．感染者数はこれまでのサンプリング方法による報告数であり実際の数ではない．

回復

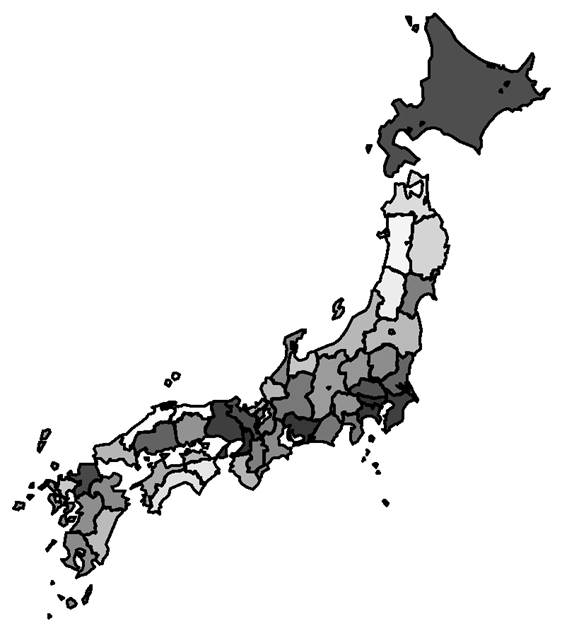
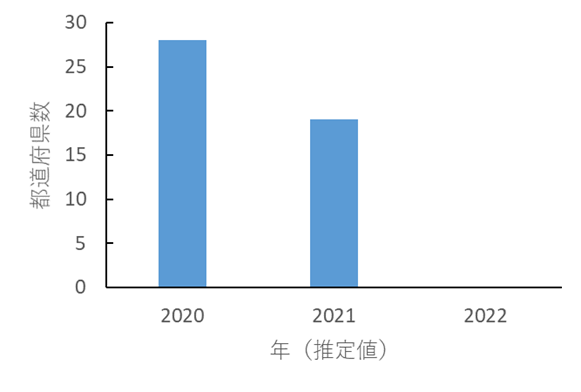
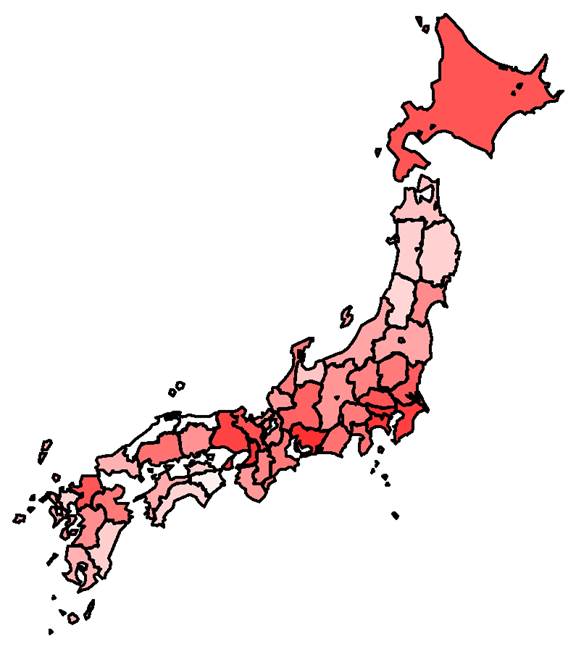
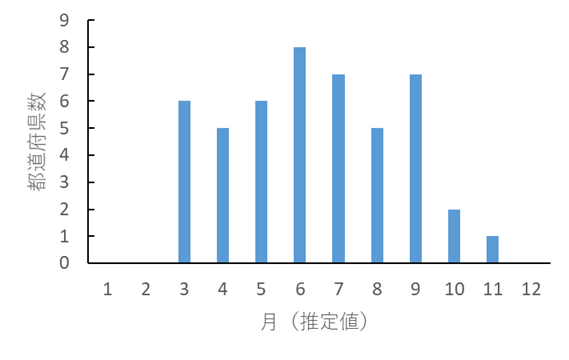
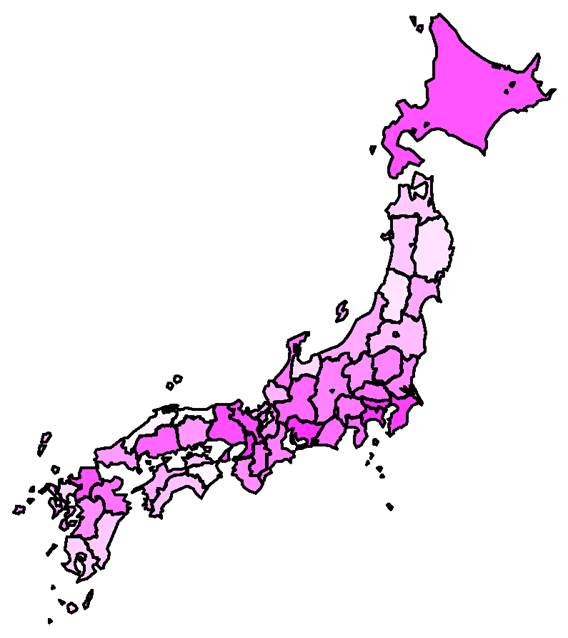
	対策による極低密度化　（< 1人） 地域のなかの感染者（infected）が1人未満（現在の調査努力量）になる時点．緑青が濃いほど早く達成されると予想された．白い部分は2022年4月以降．赤い部分は50%以上の確率で増加（増加率の対数で着色）．
社会的対策等により感染者の極低密度化に成功する時期（必ずしも根絶ではない）． 2021年9月6日を基準日とし、基準日と2021年9月27日の積算感染者数をもとにsource_sink.pdfの方法で推定したパラメーターにより予測した．基準日以前4週間以内に発見された感染者は基準日においてinfectedであると仮定している．季節性は考慮せず，人工的な免疫獲得者や既感染者の人口からの控除は行っていない．なお地域間移動は2020年7月15日から2021年3月29日までは指数関数を，それ以外は重力モデルを仮定している．今回の計算の収束は良かった．

予測される達成時期（中央値）．赤文字の地域では減少せず増加する可能性が50%以上である．季節性や人工的な免疫は考慮されていない．

	極低密度化（<1名）
都道府県	予測	都道府県	予測	都道府県	予測
鳥取県	2022年4月以降	青森県	2022年4月以降	山梨県	2022年4月以降
島根県	2022年4月以降	奈良県	2022年4月以降	宮城県	2022年4月以降
高知県	2022年4月以降	長崎県	2022年4月以降	京都府	2022年4月以降
徳島県	2022年4月以降	愛媛県	2022年4月以降	広島県	2022年4月以降
新潟県	2022年4月以降	山口県	2022年4月以降	茨城県	2022年4月以降
佐賀県	2022年4月以降	滋賀県	2022年4月以降	岐阜県	2022年4月以降
富山県	2022年4月以降	沖縄県	2022年4月以降	福岡県	2022年4月以降
和歌山県	2022年4月以降	鹿児島県	2022年4月以降	北海道	2022年4月以降
香川県	2022年4月以降	熊本県	2022年4月以降	兵庫県	2022年4月以降
秋田県	2022年4月以降	三重県	2022年4月以降	千葉県	2022年4月以降
長野県	2022年4月以降	福島県	2022年4月以降	埼玉県	2022年4月以降
宮崎県	2022年4月以降	岡山県	2022年4月以降	愛知県	2022年4月以降
山形県	2022年4月以降	群馬県	2022年4月以降	大阪府	2022年4月以降
静岡県	2022年4月以降	栃木県	2022年4月以降	神奈川県	2022年4月以降
大分県	2022年4月以降	福井県	2022年4月以降	東京都	2022年4月以降
岩手県	2022年4月以降	石川県	2022年4月以降

侵入

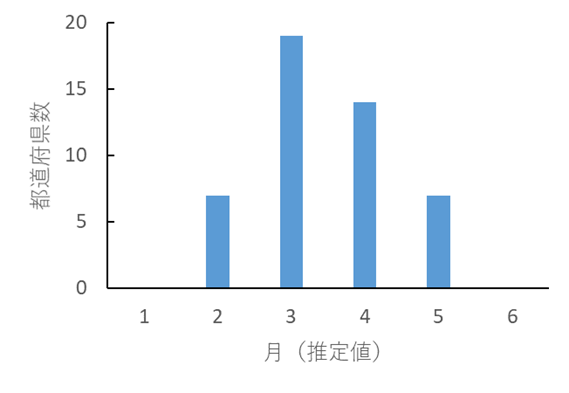
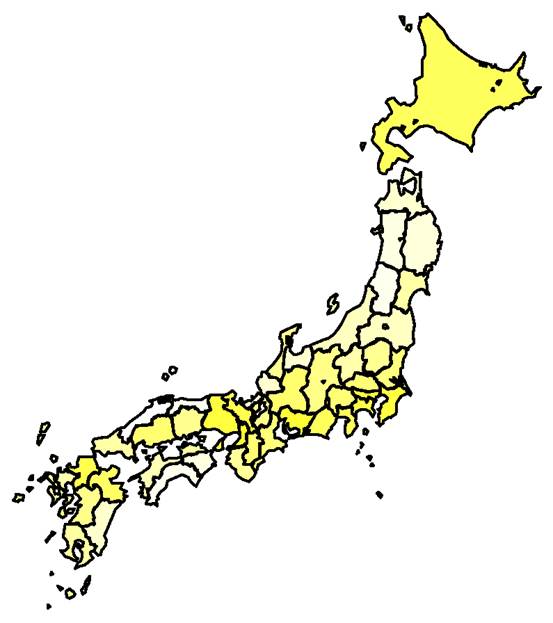
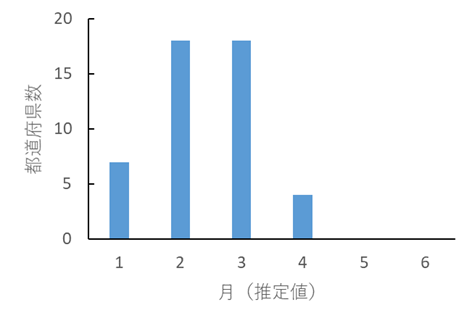
	蔓　延　（≧1000人） 感染者が1000人以上に達する時点． 色の濃いところで早くから侵入すると予測された． 標準偏差 49.1日 これまでと同じ速度で拡大し季節性もないと仮定したとき．ただし蔓延が起きない可能性のある地域も存在する．
	拡　大　（≧100人）終了 感染者が100人以上に達する時点． 色の濃いところで早くから侵入すると予測された． 標準偏差 49.1日
	定　着　（≧10人）終了 感染者が10人以上に達する時点． 色の濃いところで早くから侵入すると予測された． 標準偏差 28.5日
	到　着　終了 　国内での感染による発症がみられ始める時期． 色の濃いところで早くから侵入すると予測された． 　 国内での感染における最初の発症時点とした．可能なかぎり国内で起きた感染のみを扱うため海外での感染後の帰国や海上の船舶での感染と想定される例を除く． 標準偏差 30.4日
過去の多くの外来種の分布拡大データからパターンが類似したものを合成している．海外などからの新たな持ち込みによる国内での感染と，国内における感染の連鎖による分布拡大をともに含む．外来種に加えて初発国からの訪問者数（逆順）と都道府県人口（逆順）も教師データの一つとして投入した．定着や拡大・蔓延では前段階の到着や定着・拡大も用いている． 　実際に観察される時期は上右図の頻度分布を標準偏差で重畳した幅の広いものになる． 3月9日からは相対的な時期から年月日への変換において未達情報も考慮する方法に変更した（方法1）． （方法1：対象期間中の各日の到達／未達をデータとして，スケーリングのパラメーターと標準偏差を最尤推定）

侵入時期の相対値．赤文字は既侵入．

終了		蔓	延	（≧1	000名）	終了		拡	大	（≧100	名）
都道府県	予測 （相対値）	都道府県	予測 （相対値）	都道府県	予測 （相対値）	都道府県	予測 （相対値）	都道府県	予測 （相対値）	都道府県	予測 （相対値）
東京	0	宮城	38	山口	64.6	愛知	0	大分	35.6	山口	62.6
大阪	0.6	滋賀	38.3	新潟	65.1	東京	0.8	山梨	36.1	長崎	62.8
愛知	3.3	石川	42.5	福島	66.3	大阪	2.7	石川	36.5	鹿児島	63.2
神奈川	3.7	三重	43.5	香川	66.4	神奈川	3.4	群馬	40.1	青森	70.6
兵庫	6.7	大分	43.6	宮崎	67.2	千葉	7.7	奈良	41	富山	71.6
千葉	6.8	鹿児島	43.9	富山	72.2	兵庫	9	滋賀	44.6	香川	74.5
福岡	11.6	栃木	45	佐賀	74	京都	16.8	宮城	44.6	秋田	77
北海道	14.4	熊本	45.4	岩手	79.2	北海道	17.6	熊本	46.1	宮崎	77.6
京都	15.3	岡山	47.2	青森	83	福岡	18.7	岡山	47.5	佐賀	78.5
埼玉	16.6	山梨	47.9	高知	84.9	埼玉	18.9	長野	49.2	岩手	78.7
広島	23.9	群馬	49.3	徳島	88.3	茨城	21.8	沖縄	50	高知	79.6
茨城	25.7	長野	51.9	山形	91.2	岐阜	24.2	和歌山	50.4	山形	80.2
静岡	33.5	長崎	52.8	秋田	94.8	静岡	31.8	福井	51	徳島	93.2
岐阜	34.8	愛媛	59	島根	98.7	広島	31.9	新潟	56.6	鳥取	98
沖縄	35.4	和歌山	63.9	鳥取	100	栃木	34.8	福島	57.2	島根	100
奈良	38	福井	64.5			三重	35.4	愛媛	59.8

終了		定	着	（≧10	名）	終了		到	着
都道府県	予測 （相対値）	都道府県	予測 （相対値）	都道府県	予測 （相対値）	都道府県	予測 （相対値）	都道府県	予測 （相対値）	都道府県	予測 （相対値）
東京	0	奈良	38	山口	64.5	大阪	0	三重	34.5	佐賀	59.8
大阪	0.6	滋賀	38.3	新潟	65.1	愛知	2.7	沖縄	35.5	愛媛	64.4
愛知	3.3	石川	42.4	福島	66.2	東京	3.6	茨城	36.5	新潟	68.6
神奈川	3.7	三重	43.5	香川	66.4	兵庫	7	長野	42.1	福島	70
兵庫	6.7	大分	43.6	宮崎	67.2	千葉	7.8	熊本	43.2	宮崎	75.6
千葉	6.8	鹿児島	43.8	富山	72.1	神奈川	9.7	滋賀	44.6	青森	76.7
福岡	11.5	栃木	45	佐賀	74	福岡	13.3	岡山	45.2	福井	76.9
北海道	14.3	熊本	45.4	岩手	79.2	京都	15	石川	46.4	富山	77.4
京都	15.3	岡山	47.2	青森	82.9	静岡	20.5	栃木	47.1	岩手	82.5
埼玉	16.5	山梨	47.9	高知	84.9	北海道	21.2	和歌山	50.3	秋田	85.5
広島	23.8	群馬	49.2	徳島	88.3	大分	25.3	長崎	51.9	徳島	85.8
茨城	25.6	長野	51.9	山形	91.2	岐阜	29.5	香川	53.8	山形	91.7
静岡	33.6	長崎	52.8	秋田	94.7	広島	30.9	鹿児島	54.1	高知	92.1
岐阜	34.7	愛媛	59	島根	98.6	奈良	31.4	山口	56.1	鳥取	92.9
沖縄	35.4	和歌山	63.9	鳥取	100	山梨	32.9	宮城	56.5	島根	100
宮城	38	福井	64.3			埼玉	34.1	群馬	59.2

過去の予測はこちら

再拡大が開始する直前のページ

概　況

１．増減の位相の地域差は大きいが，2020年4月のピーク（第１ピーク）のあと減少し，7月には再び感染が急拡大したが（第２ピーク），8月以降は全国として減少した．9月29日の計算から反転して拡大し（第３ピーク），2021年1月中旬の計算から減少した．2021年3月7日の計算から反転して増加期に入り（第４ピーク），4月20日の計算をピークとして増加率が低下してきた．
最近では2021年7月5日の計算から増加に転じた（第5ピーク）．2021年8月16日の計算をピークとして増加率の低下が続いている．導入された場合に感染者が増加する可能性のある地域は3都府県である（週あたり増加率＞1.0である可能性が50%以上）．

２．　これから集団のvaccinationが進むと，変異株の中では抵抗性を持つものが相対的に有利になるが，抵抗性を持たず単に増加率が大きい変異株もvaccinationを行っていない少数の人口で増加が可能である．オリンピックの時点で日本にはvaccinationが行われた人と行われていない人が混在する．そこにオリンピックで世界各地の変異株が導入された場合は，世界の変異株の増加率をvaccinationの有無の効果とともに共通の環境で比較できる（変異株の競技会）．各変異株の増減の状況を東京で網羅的にモニタリングすることにより，これから世界で優占する変異株を予測して効果的な対策を立てることが可能性になるかもしれない．またこのモニタリングは国内での早期警戒のためにも望ましい．

３．2021年8月下旬において感染拡大初期に相当するニュージーランドやオーストラリアでは厳しい社会抑制の下で増加しているのに対して，日本で抑制傾向にある理由は不明．とても感染が起きやすい場所で感染が一巡したか，あるいはそのような場所での集中的なvaccinationが機能したか（イメージの説明susceptibility.pdf）．
　また2020年8月に減少した理由も不明．皆の自粛による社会的抑制か，とても高密度で感染が起きやすい場所では感染が一巡して局地的に集団免疫が形成されたか（イメージの説明susceptibility.pdf），あるいはそのような場所での局地的な対策が機能したか，梅雨明け後の気候によるのか．　

４．抑制が進行した段階では，もういちどソースとなる地域や経路を再点検し，見逃されてきた地域や経路があれば重点的に対応することでソースとなる場所や場面全体への対策が進む可能性がある．

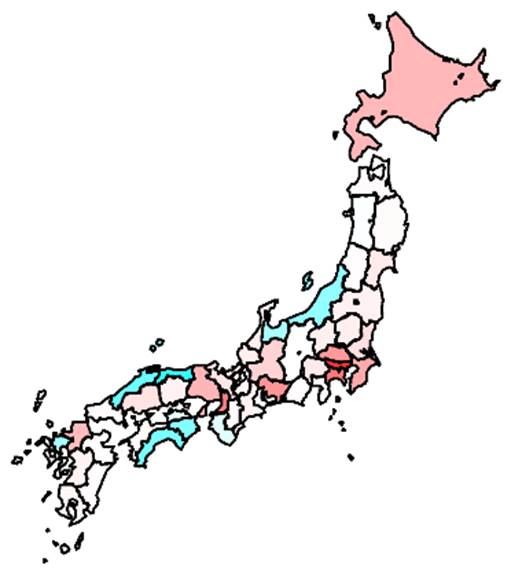
５．人口密度が高い都道府県が感染のソース（供給地，下図の赤色）となり，人口密度が低い都道府県ではシンク（導入により散発的に発生するが維持されない地域，下図の青色）となる可能性がある（source_sink.pdf）．一般的にソース地域での集中的な対策がシンク地域にとっての対策にもなる．

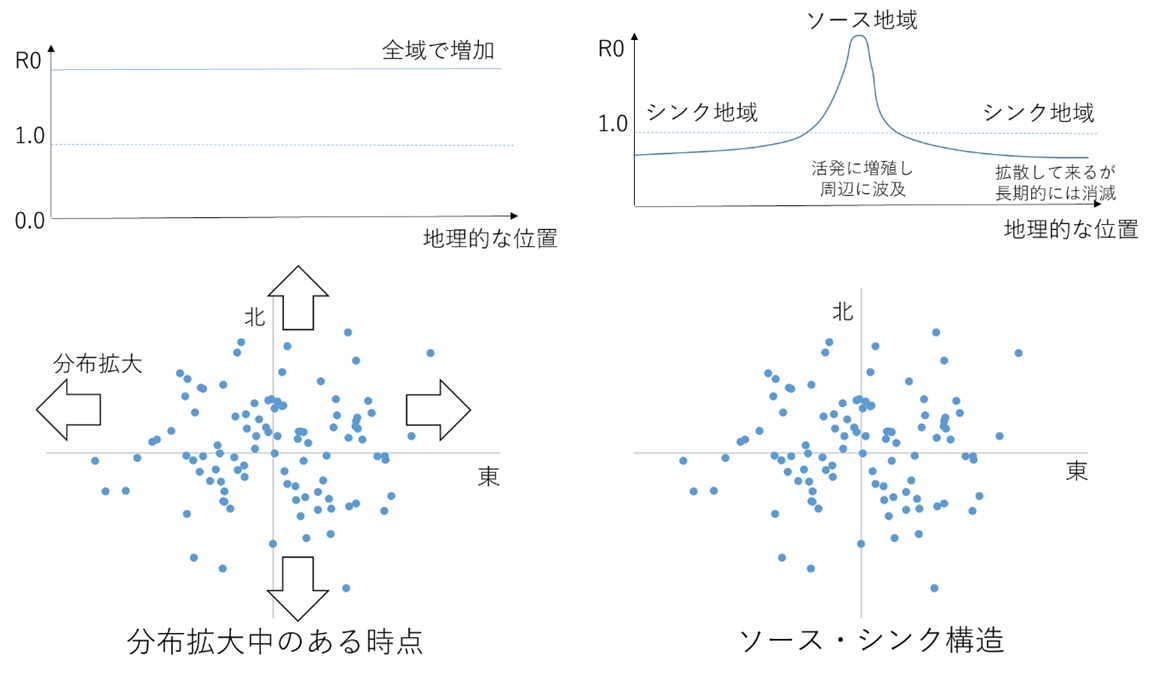
	外来生物の地理分布では，分布の中心で外来生物や感染者の密度が高く，周辺で密度が低いパターンが見られることが多い（下図）．このような類似した地理分布は２つのメカニズムで出現する．ひとつは活発な増殖と拡散の一時点であり（下図左），もうひとつはソース・シンク構造である（下図右）． 　対策として下図左では全域でのR0低下と分布拡大の先端でのemergency controlが行われるが，下図右ではソース地域に集中したR0低下対策で個体群全体が根絶されることもある． 　ただし増殖しやすい変異の出現により潜在的なソース地域が拡大する可能性がある．

望ましいこと

１．重症者数は新規感染者数から約13日の遅れをもつので（下図の推定では16日遅れ），2週間先までの予測は容易であり，先回りした対策が可能である．2021年7月26日の時点での重症者数は7月13日ころの新規感染者を反映している．また2021年7月26日の新規感染者（既知）から予測した2021年8月8日（山の日）の東京都の重症者数はおよそ153名程度である（78×7月26日新規感染者週平均／7月13日新規感染者週平均）．なお8月8日まで現在と同じ状況が続くと（13日間で新規感染者数が1.97倍），仮にそれ以降新規感染者が減少しても8月21日の重症者数はおよそ300名となる．

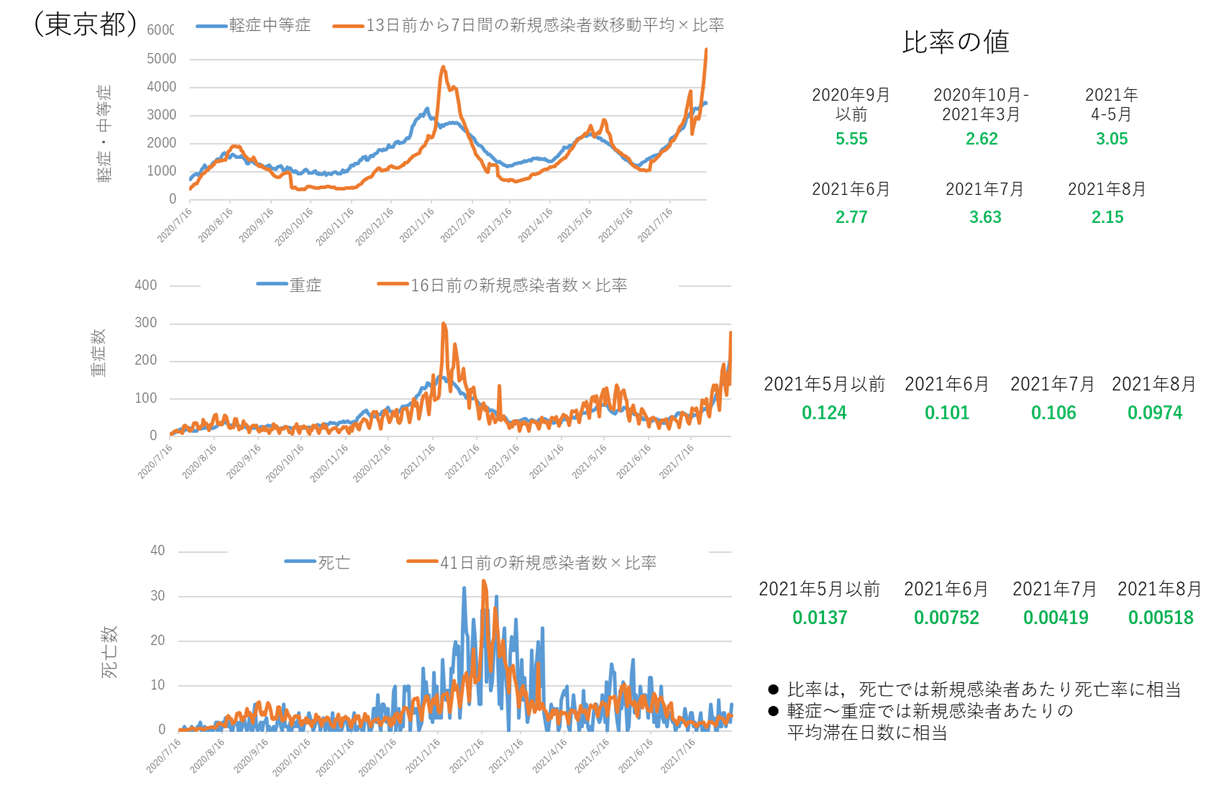
2．隔離効果（検査とクラスター対策）×社会的抑制効果（リモートワークなど）×集団免疫効果（回復者やワクチン）を必要な値に保ちながら，隔離コスト（感染者数に比例）＋社会的抑制コスト（感染者数によらない）＋集団免疫コストを小さくすることになるのかもしれない．総合的な対策も有効．上記の総合的な効果値が同じであっても，多くの感染者が存在する状態と，ほとんど感染者が存在しない状態があり得る（説明measure.pdf）．隔離により対応できれば社会的抑制よりコスト効率が良く波及効果も含めて経済成長に寄与する可能性がある．感染者密度の管理目標を決めて合意しておくと良いと思われる（感染者密度の管理目標option.pdf）．もし抵抗性の変異株などによりvaccinationによる集団免疫が十分でなければ，人工的な免疫の効果と社会的抑制や隔離を組み合わせて対応することになる．

3．ある感染者について自分が感染した場面と他者を感染させた場面（なし〜複数）の情報が同時に得られれば，世代を時間の単位として次元が感染場面×感染場面のprojection matrixを作成し（例：飲食店で感染した１名が平均して家庭内で○名，オフィスで○名感染させる），最大固有値のsensitivityとして経路の重要度を評価して合意形成に利用できるかもしれない．（個体群の行列モデル．経路不明は感染場面のひとつとしておき，仮定をおいてR0＝最大固有値となるよう逆推定するか）

4．在来株での大都市圏での週あたり増加率の最大はおよそ1.3倍だったが変異により増殖パラメーターが増加している（Alpha株について神戸市kobe2021.pdf，全国japan2021feb_march.pdf）．最近のDelta株では社会抑制のみを行う場合は80%以上の抑制が最低限になり減速は可能であるが増加を止めることが難しくなる可能性があり， vaccinationや高リスク者への対策を組み合わせることが重要かもしれない．

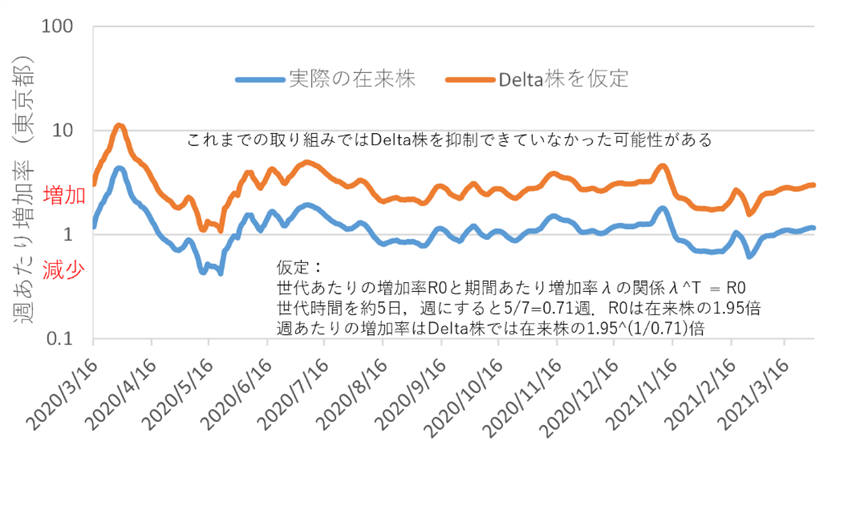
　ただし入院や死亡などで選択的に変異が除去されるため，特殊な状況を除いて重症化する方向の進化は考えにくい（例外は増殖パラメーターの増加と重症化がリンクして後者の負荷を打ち消すとき．感染しなかった層に感染するようになり，その層が重症化しやすい場合など．ウイルスの立場では感染しなかった層は身近な未利用資源）．

5．基本的には，ソース地域となっている大都市圏の人口密集地で集中的な対策をとり，感染が起きる場面と地域を絞り込むことで社会的影響とコストを限定化できる．https://www.stat.go.jp/data/chiri/map/c_koku/t-mitsu/index.html
ただしR0の大きな変異株が出現したためソース地域はこれまでより広がっている．

6．一般的に高い人口密度は急激な感染拡大をもたらす可能性があるため，長期的には地方に分散して居住し，都市に人口が集中しない社会をつくることが望ましい．

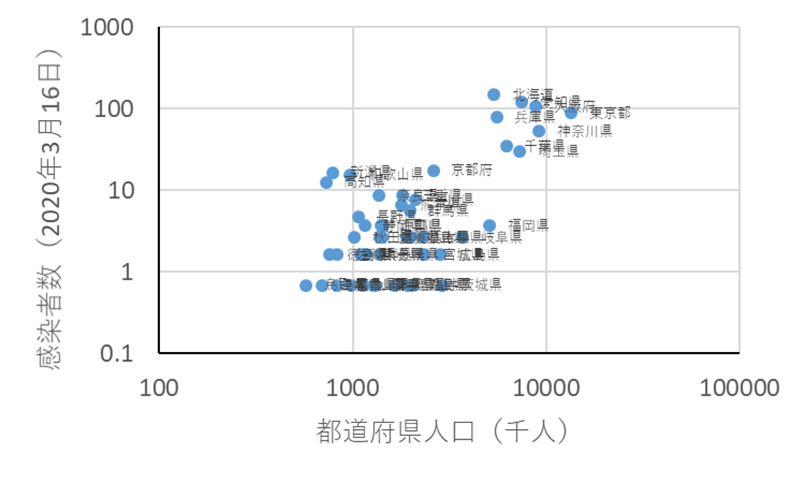
COVID-19での人口と感染者数の関係（両対数目盛）．より正確には人口の代わりに平均混み合い度（自分の周囲の人数を全員で平均する）を用いることが望ましい．人口が多い都道府県では人口当たりの感染者数が多い傾向がありそうだ． 回帰曲線：　（感染者数）＝10^-4.0×（人口千人）^1.4 　なお飛火的な分布の可能性がある地域（高知，和歌山，新潟）を除いたreduced major axis法では　（感染者数）＝10^-6.4×（人口千人）^2.1であり人口が10倍になると感染者は100倍になる．

7．新興感染症の可能性も想定した野生動物との望ましい共存関係を考えることが望ましい．

8．国際的にbiosecurityを遵守する状況を作ることが望ましい（認証制度など）．

掲載日：2020年2月15日，2021年9月28日更新

計算方法：　

・これまで知られている外来生物の分布拡大パターンの中から初期の分布拡大パターンが新型コロナウイルス感染症に類似した種を抽出し，これを合成することで予測を行った．外来種に加えて初発国からの訪問者数（逆順）（日本政府観光局https://statistics.jnto.go.jp/graph/#graph--inbound--prefecture--ranking）と都道府県人口（逆順）も教師データとして投入した．
・計算には「みんなでGIS」の応用プログラム「外来生物侵入順序解析」を使用した．詳細や信頼性の評価はKoike & Morimoto 2018参照．

・2020年4月12日以降は個体群モデル（SIRモデル）に都道府県間の移動を組み込んだ状態空間モデルも利用している（source_sink.pdf）．

予測計算，種特性の記載，概況，注意・警戒事項の記載者：　　小池文人（横浜国大），既分布の外来生物の分布拡大データは森本信生（畜産草地研究所），および昆虫情報処理研究会のゴケグモ類の情報センター，厚生労働省による過去の新型インフルエンザ情報（過去のまとめ検証用），環境省のヒアリに関する諸情報について，農林水産省のCSF感染野生イノシシの発見地点などによる．ＣＯＶＩＤ−１９の感染者数の情報は各都道府県ホームページのほか朝日新聞と日経新聞の集計による．

　

文献：

Koike, F. and Morimoto, N. 2018. Supervised forecasting of the range expansion of novel non-indigenous organisms: alien pest organisms and the 2009 H1N1 flu pandemic. Global Ecology and Biogeography 27:991–1000. https://doi.org/10.1111/geb.12754

アンドロイド端末で文字化けが起きる場合は[設定]，[端末管理]，[アプリ]から[Google]の[ストレージ]で[キャッシュを消去]してみてください．

ホームへ