過去のページです

現在のページはこちら

新型コロナウイルス感染症COVID-19

英名：　Novel Coronavirus Disease 2019

病原体：　SARS-CoV-2

原産地・生態： ヒトの感染症．2019年末に中国武漢市周辺から分布拡大．野生脊椎動物に感染するウイルスがヒトへの感染能力を獲得したと考えられている．季節性は不明．

情報源

厚生労働省:　 新型コロナウイルス感染症についてhttps://www.mhlw.go.jp/stf/seisakunitsuite/bunya/0000164708_00001.html

将来予測

2020年6月16日時点

これらの予測はひとつの方法によるものであって誤差を含み，今後の感染拡大防止策などにより変化すると考えられる．また季節性は考慮されていない．感染者数はこれまでのサンプリング方法による報告数であり実際の数ではない．

回復

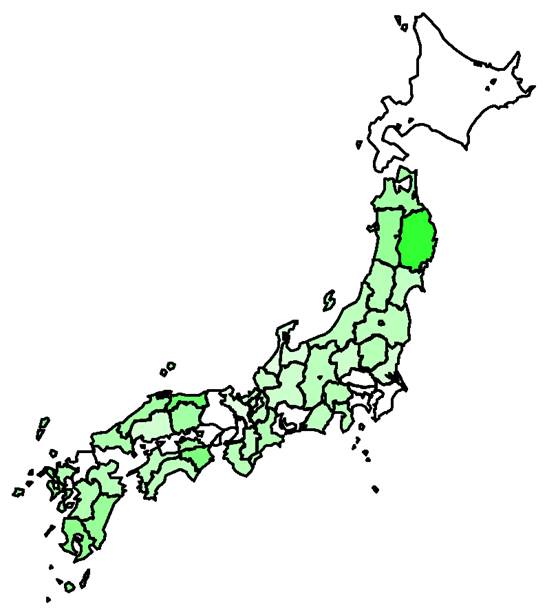
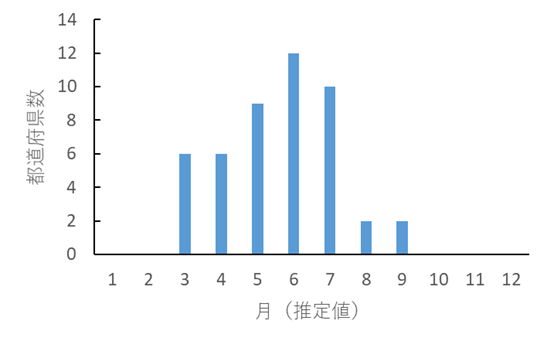
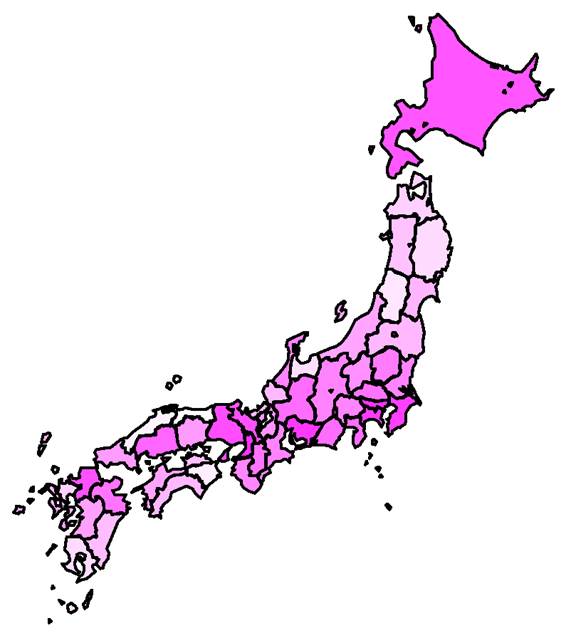
	対策による極低密度化　（< 1人） 緑が濃いほど早く達成されると予想された．地域のなかの感染者（infected）が1人未満（現在の調査努力量）になる時点．白い部分は2020年12月以降．
緊急事態宣言下の社会的対策により感染者の極低密度化に成功する時期（必ずしも根絶ではない．中国や韓国，台湾，ニュージーランドなどの状態）．実際の感染者数は不明のため5月25日の積算感染者数が全てinfectedであったと仮定して，2020年5月25日と6月15日の積算感染者数をもとにsource_sink.pdfの方法で推定したパラメーターにより予測した（人口密度の評価などに改善の余地がある）．季節性は考慮されていない．

予測される達成時期．赤文字の地域では必ずしも減少しない可能性がある（ただしこの期間のパラメーターでは全て減少）．季節性は考慮されていない．

		極低密度化	（<1名）
都道府県	予測	都道府県	予測	都道府県	予測
岩手県	4月	山形県	9月	岐阜県	10月
鳥取県	6月	大分県	9月	広島県	11月
徳島県	7月	栃木県	9月	茨城県	11月
鹿児島県	8月	山梨県	9月	富山県	11月
秋田県	8月	高知県	10月	石川県	11月
宮崎県	8月	新潟県	10月	京都府	11月
長崎県	8月	長野県	10月	福岡県	12月以降
島根県	8月	静岡県	10月	北海道	12月以降
香川県	8月	愛媛県	10月	兵庫県	12月以降
青森県	8月	福島県	10月	千葉県	12月以降
岡山県	8月	奈良県	10月	埼玉県	12月以降
山口県	9月	滋賀県	10月	愛知県	12月以降
佐賀県	9月	宮城県	10月	大阪府	12月以降
熊本県	9月	福井県	10月	神奈川県	12月以降
三重県	9月	沖縄県	10月	東京都	12月以降
和歌山県	9月	群馬県	10月

侵入

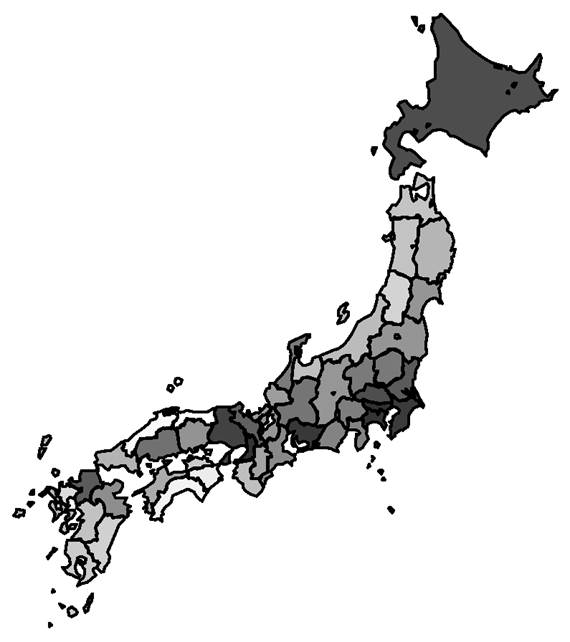
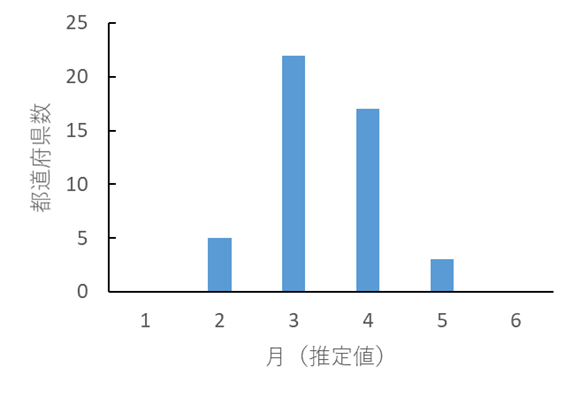
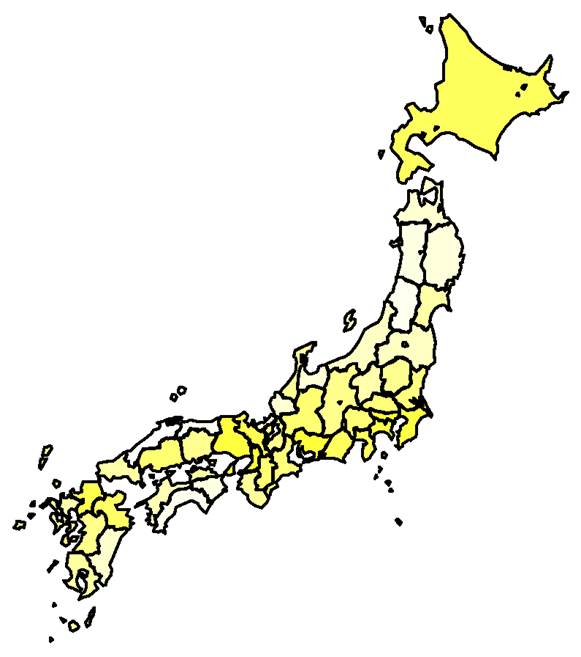
	蔓　延　（≧1000人） 感染者が1000人以上に達する時点． 色の濃いところで早くから侵入すると予測された． 標準偏差 28.1日 これまでと同じ速度で拡大し季節性もないと仮定したとき．ただし蔓延が起きない可能性のある地域もある．
	拡　大　（≧100人） 感染者が100人以上に達する時点． 色の濃いところで早くから侵入すると予測された． 標準偏差 31.1日
	定　着　（≧10人） 感染者が10人以上に達する時点． 色の濃いところで早くから侵入すると予測された． 標準偏差 18.4日
	到　着 　国内での感染による発症がみられ始める時期． 色の濃いところで早くから侵入すると予測された． 　 国内での感染における最初の発症時点とした．可能なかぎり国内で起きた感染のみを扱うため海外での感染後の帰国や海上の船舶での感染と想定される例を除く． 標準偏差 22.9日
過去の多くの外来種の分布拡大データからパターンが類似したものを合成している．海外などからの新たな持ち込みによる国内での感染と，国内における感染の連鎖による分布拡大をともに含む．外来種に加えて初発国からの訪問者数（逆順）と都道府県人口（逆順）も教師データの一つとして投入した．定着や拡大・蔓延では前段階の到着や定着・拡大も用いている． 　実際に観察される時期は上右図の頻度分布を標準偏差で重畳した幅の広いものになる． 3月9日からは相対的な時期から年月日への変換において未達情報も考慮する方法に変更した（方法1）． （方法1：対象期間中の各日の到達／未達をデータとして，スケーリングのパラメーターと標準偏差を最尤推定）

侵入時期の相対値．赤文字は既侵入．青文字は人口密度が低いため2020年3月と同様の状況でも蔓延しない可能性がある地域（ただし家族や職場などでの局地的な感染拡大はありうる．また地域の同定には改善の余地がある）．

		蔓	延	（≧1	000名）			拡	大	（≧100	名）
都道府県	予測 （相対値）	都道府県	予測 （相対値）	都道府県	予測 （相対値）	都道府県	予測 （相対値）	都道府県	予測 （相対値）	都道府県	予測 （相対値）
東京	0	山梨	37.7	新潟	67.3	東京	0	大分	36.4	長崎	60.1
大阪	1.1	静岡	40.2	和歌山	68.6	大阪	0.8	三重	36.5	山口	62.1
神奈川	2.4	三重	42.9	富山	69	愛知	0.9	石川	37.1	青森	68.3
愛知	3.7	沖縄	42.9	熊本	70.4	神奈川	1.7	山梨	38.3	鹿児島	68.6
千葉	5.2	大分	45	秋田	71.1	千葉	5.3	岡山	44.3	秋田	72
兵庫	8.3	岡山	47.7	青森	71.5	兵庫	6.5	沖縄	44.5	宮崎	72.3
北海道	13.7	福島	48.7	香川	74.7	北海道	14.2	宮城	44.6	岩手	73.1
埼玉	14.5	宮城	49	鹿児島	75.2	福岡	15.8	奈良	45.9	高知	73.3
茨城	20	長野	49.2	宮崎	77.3	埼玉	15.9	福井	47.7	香川	74.4
福岡	20.6	滋賀	49.2	山形	78.9	京都	16.3	滋賀	49.5	富山	75.6
京都	23.2	福井	52.6	佐賀	83.2	茨城	22.3	和歌山	51	山形	77.7
広島	31.4	奈良	56.1	徳島	91.2	岐阜	24.3	長野	51.1	佐賀	79.6
岐阜	33	愛媛	59.6	高知	94	広島	28.2	熊本	51.6	徳島	92.4
栃木	35.3	山口	63.1	島根	97.7	栃木	31.2	愛媛	53.9	島根	97.8
石川	35.6	岩手	64.2	鳥取	100	静岡	34.7	福島	54.1	鳥取	100
群馬	35.8	長崎	64.7			群馬	35.4	新潟	59

		定	着	（≧10	名）			到	着
都道府県	予測 （相対値）	都道府県	予測 （相対値）	都道府県	予測 （相対値）	都道府県	予測 （相対値）	都道府県	予測 （相対値）	都道府県	予測 （相対値）
大阪	0	栃木	36.6	高知	65	大阪	0	沖縄	35.4	群馬	60.3
東京	0.6	石川	39.9	福井	65.5	愛知	3.5	三重	35.6	愛媛	64.5
愛知	3.4	長野	40	福島	65.7	東京	3.9	茨城	37.7	福島	70.1
神奈川	5.2	茨城	40.1	香川	67.7	兵庫	7	熊本	43.1	新潟	71.4
千葉	7.4	三重	40.1	宮崎	67.9	千葉	7.8	長野	43.4	宮崎	75.6
兵庫	14	山梨	40.9	秋田	70.8	神奈川	10.3	岡山	45.3	青森	76.7
京都	15.8	和歌山	41.6	青森	77.7	福岡	13.4	滋賀	45.7	福井	79
福岡	15.8	群馬	46.4	佐賀	77.9	京都	15.7	栃木	47	富山	79.4
北海道	18	滋賀	48.1	鹿児島	82.1	北海道	21.2	石川	47.7	岩手	82.6
広島	25.4	岡山	51	岩手	82.3	静岡	21.2	和歌山	50.2	秋田	85.6
岐阜	29.3	山口	51.6	富山	84.7	大分	25.3	長崎	51.8	徳島	85.8
静岡	29.6	熊本	54.1	山形	87.6	岐阜	30.7	香川	53.8	山形	91.8
埼玉	31.7	愛媛	55.7	徳島	92.1	広島	30.9	鹿児島	54.1	高知	92.1
大分	32.7	新潟	56.3	島根	94	奈良	31.2	山口	56.1	鳥取	93
沖縄	32.7	長崎	63.4	鳥取	100	山梨	33.7	宮城	56.4	島根	100
奈良	33	宮城	64			埼玉	35	佐賀	59.7

過去の予測はこちら

概　況

１．世界最大の東京都市圏と阪神都市圏，北海道などで新しい感染者が発生している．大都市圏の外縁と地方の政令市等をあわせて40%の都道府県で拡大期に達した．抑制されている地域も含めて約94％の都道府県で定着し，国内での感染による発症が約98%の都道府県で確認された．

２．感染者の報告数は全ての都道府県で減少している．地域間移動の影響は2020年3月16日から4月6日に至る期間では個体群モデル（空間明示的ＳＩＲモデル）で検出されたが，その後は現在に至るまで検出されていない．

３．収束に向かう場面では予測侵入時期は先延ばしとなってゆく．個体群モデルによる極低密度達成時期の予測では，人口密度が低い地域の一部で増加が観察されると，他地域でも起きうると評価され高密度地域の予測時期が遅れる傾向がある．

４．感染者の減少は気温上昇期と重なっているため単純統計では社会的対策と気温を分離できない．別のアプローチでの検証が望ましい． 仮に気温上昇による抑制であり，感受性を持つ人口の減少が進行しなかった場合は，2020/2021年冬に厳しい蔓延が予想される．

５．未確認の例が多いと考えられている．未確認例が多いことは将来予測において病院やホテルなどでの隔離をそれほど考慮する必要がないことを意味する（隔離があまり機能していない可能性がある）．また念のためCOVID-19に特定しない死亡統計のモニタリングも望ましい．

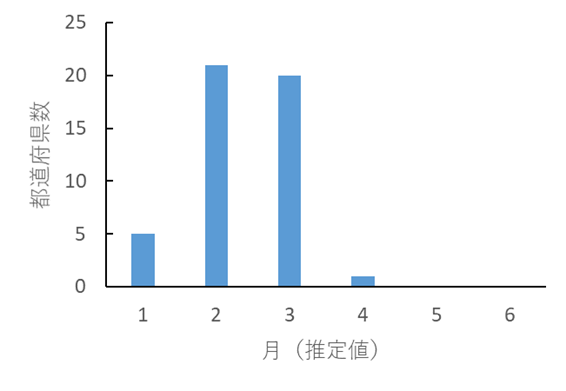
６．海外からの到着によると考えられる初期の国内での感染は発症の時期が1月下旬から2月初めに集中していた．計算上のweightとして初発国からの訪問者数の寄与が最も大きかったことや，それに次いでweightが大きかったのは同地域からの他の外来生物（ヒアリ）であったことから，初発国からの訪問者数がこの時期に集中したことによる可能性がある．

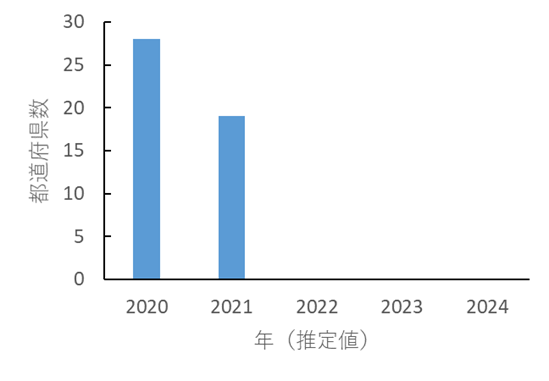
７．その後の定着では（2020年2月26日時点において10名以上），その時点で大阪や京都，神戸などでは定着しなかったとすると， 2月上旬頃までに日本全国で合計およそ10.5回くらい定着したのかもしれない（方法2）．同様の方法で計算した到着数（1月下旬から2月上旬に発症）を用いると，定着／到着の比率は68％程度になる．
（方法2：都道府県への定着の有無を目的変数としたlogistic回帰から-ln(1-p)で計算．説明変数では人口のみが有意で人口の多い都道府県に定着しやすい．初期の到着において重要であった訪問者数は，定着では有意でなかった）

８．2月中旬以降に国内の大都市域から地方への分布拡大が始まっていた可能性がある．

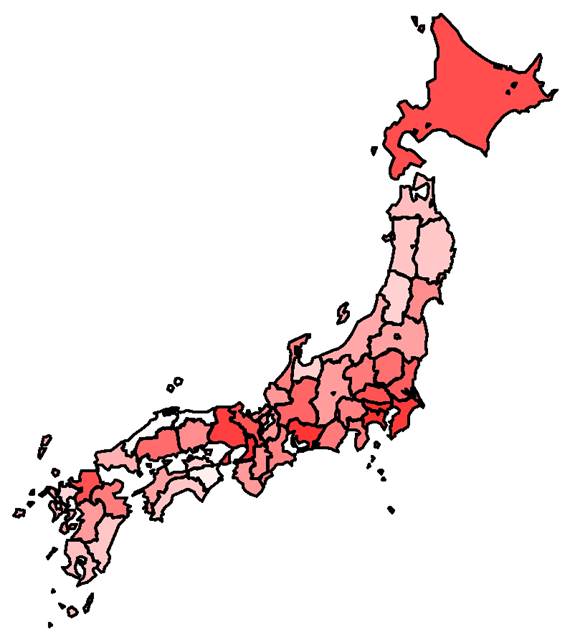
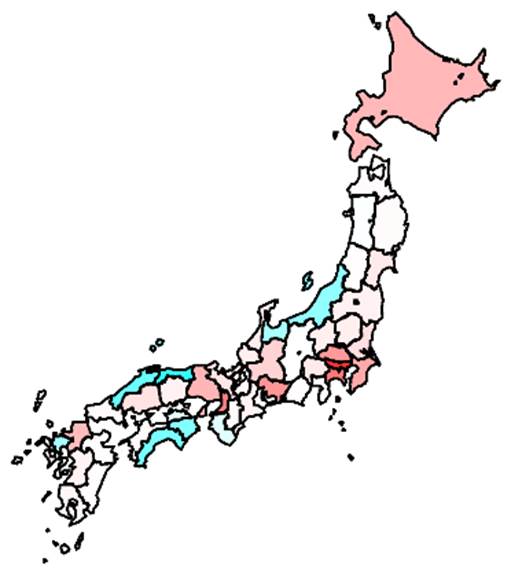
９．定着では飛び火的な分布が見られた（地理的な遠近でなく予測から乖離した出現）．拡大では人口が重要だが一部の地域で散発的な感染者増加が見られる．蔓延は人口がとても重要で予測性が高い．人口密度が高い都道府県が感染のソース（供給地，下図の赤色）となり，人口密度が低い都道府県ではシンク（導入により散発的に発生するが維持されない地域，下図の青色）となる可能性がある（source_sink.pdf）．一般的にソース地域での集中的な対策がシンク地域にとっての対策にもなる．

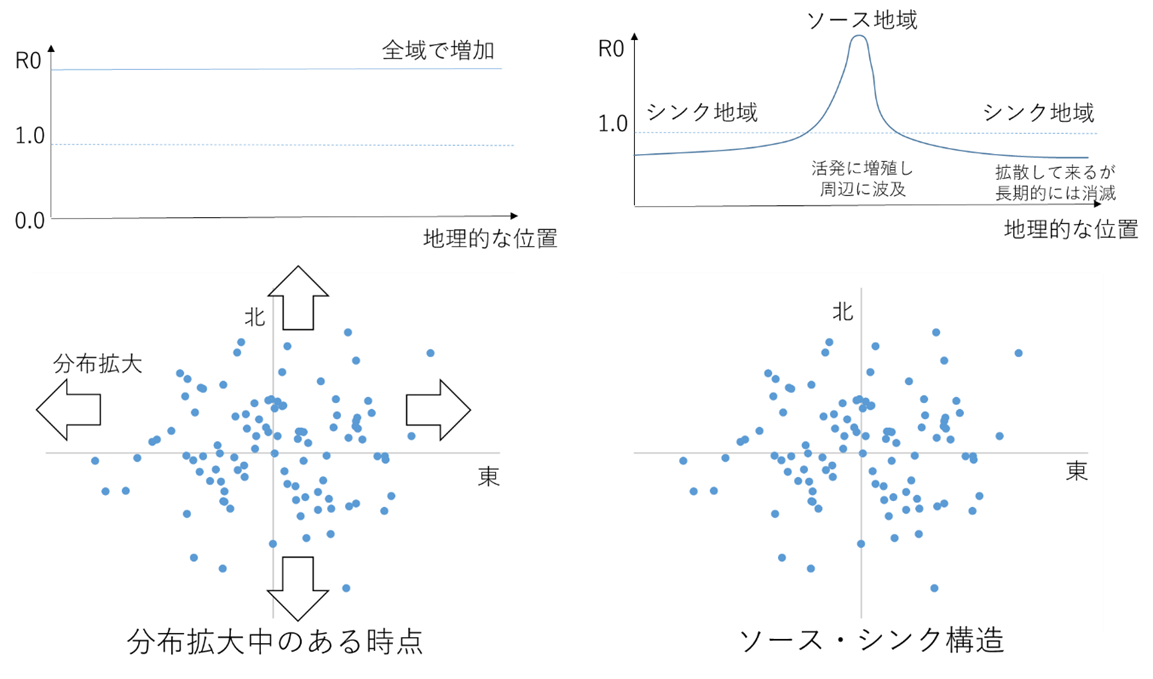
	外来生物の地理分布では，分布の中心で外来生物や感染者の密度が高く，周辺で密度が低いパターンが見られることが多い（下図）．このような類似した地理分布は２つのメカニズムで出現する．ひとつは活発な増殖と拡散の一時点であり（下図左），もうひとつはソース・シンク構造である（下図右）． 　対策として下図左では全域でのR0低下と分布拡大の先端でのemergency controlが行われるが，下図右ではソース地域に集中したR0低下対策で個体群全体が根絶されることもある．

１０．他者に感染する能力を持つ期間が長い可能性があり，増殖速度のパラメーターであるR₀=λ^Tの中で世代時間Tが長く， 世代あたり増加率R₀に比べて1日あたり平均の増加率λが小さい可能性がある． R₀=Σl_x m_xに相当するl_x（感染x日後にinfectedのままである確率）とm_x（感染x日後に他者に感染させる数）は不明．

望ましいこと

１．人口密度の2乗に比例して感染者が増えるため，東京都市圏の高人口密度地域では厳しい社会的手段（集中や接触の抑制，隔離，移動抑制など）をとり，周辺地域（クラスター対策地域）から支援してゆくことが望ましいかもしれない．約1週間の遅れをもつ正のフィードバックであり，感染者数を指数関数で予測した1週間後の値が現在の本当の姿である．https://www.stat.go.jp/data/chiri/map/c_koku/t-mitsu/index.html

２．社会活動の継続性と量的な感染症拡大遅延対策（R₀抑制，空間拡大抑制など）のバランスを取るには，ランダムサンプリング等によるsusceptible, infected, recoveredの各人数のモニタリング結果をもとに，社会的な対策手段（休校や隔離のような集中や接触の抑制，移動抑制，など）を組み合わせて，重症のinfectedが受け入れ可能な人数以下に保たれるよう，正のフィードバックを行うシステム（実際の感染）を操縦することになる．短期的な管理目標をみなで共有すると良いかもしれない（例：1週間後の新規感染者の予測数を目標値以下にする，指数関数的増加がみられない状態にする，など）．

３．このためには，社会的な対策手段を組み込んだ感染症の動態モデルでの数値予測（かつて新型インフルエンザ対策として研究された）で目標を達成できると予想される対策手段の組み合わせの中で，社会の動態モデル（産業間の労力，原材料，輸送力等サービスなどの感受性による連関マトリックス等，必ずしもお金ではない）によって社会活動に影響が少なく蔓延下の巨大都市でも持続可能なシステムをデザインすると良いかもしれない．

4．社会的な対策（接触抑制や移動抑制など）を終了するには，(1)医学的な解決方法（ワクチンや治療薬など）が普及するか， (2)多数の感染により集団免疫を獲得すること（感受性を持った人口の密度が閾値を下回る状態），あるいは(3)極低密度化に成功すること（中国，韓国，台湾，ニュージーランドなど．source-sink構造を利用すれば可能性あり）が必要．それまでは社会的な抑制が継続するため，抑制に適応した業態や産業の立ち上げを急ぐと良いかもしれない（r戦略）．変化が難しい場合は事業の休眠が選択肢になる（乾燥地植物のような予測できない環境での休眠戦略．固定費凍結と不動産所有者も含めて関係者の政府による一時雇用・派遣事業など．収束後に増税）．治療薬は長い可能性がある世代時間T(serial interval相当）を短縮できればR₀を低下させ得る．

5．社会活動の継続性のため，場合によっては重症化するリスクに応じて30代以下など若手の担当者に社会活動を託すことができる態勢を考えても良いのかもしれない．

http://weekly.chinacdc.cn/en/article/id/e53946e2-c6c4-41e9-9a9b-fea8db1a8f51

6．一般的に高い人口密度は急激な感染拡大をもたらす可能性があるため，長期的には地方に分散して居住し，都市に人口が集中しない社会をつくることが望ましい．

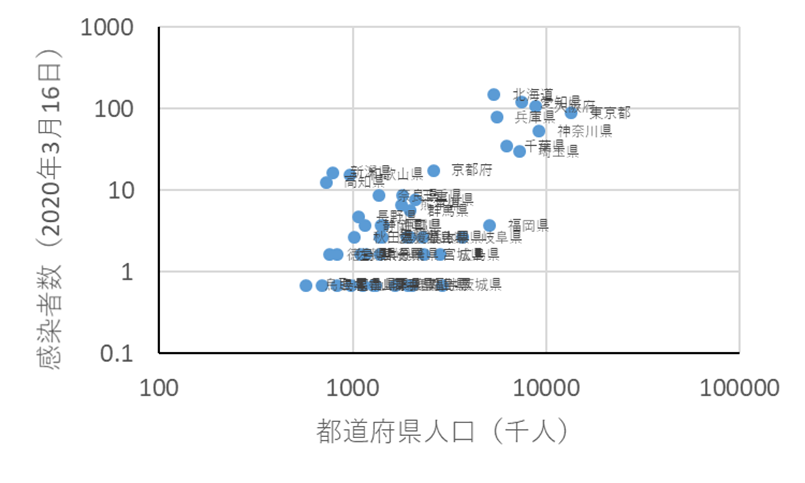
COVID-19での人口と感染者数の関係（両対数目盛）．より正確には人口の代わりに平均混み合い度（自分の周囲の人数を全員で平均する）を用いることが望ましい．人口が多い都道府県では人口当たりの感染者数が多い傾向がありそうだ． 回帰曲線：　（感染者数）＝10^-4.0×（人口千人）^1.4 　なお飛火的な分布の可能性がある地域（高知，和歌山，新潟）を除いたreduced major axis法では　（感染者数）＝10^-6.4×（人口千人）^2.1であり人口が10倍になると感染者は100倍になる．

7．新興感染症の可能性も想定した野生動物との望ましい共存関係を考えることが望ましい．

8．国際的にbiosecurityを遵守する状況を作ることが望ましい（認証制度など）．

掲載日：2020年2月15日，2020年6月16日更新

計算方法：　

・これまで知られている外来生物の分布拡大パターンの中から初期の分布拡大パターンが新型コロナウイルス感染症に類似した種を抽出し，これを合成することで予測を行った．外来種に加えて初発国からの訪問者数（逆順）（日本政府観光局https://statistics.jnto.go.jp/graph/#graph--inbound--prefecture--ranking）と都道府県人口（逆順）も教師データとして投入した．
・計算には「みんなでGIS」の応用プログラム「外来生物侵入順序解析」を使用した．詳細や信頼性の評価はKoike & Morimoto 2018参照．

・2020年4月12日以降は個体群モデル（SIRモデル）に都道府県間の移動を組み込んだ状態空間モデルも利用している（source_sink.pdf）．

予測計算，種特性の記載，概況，注意・警戒事項の記載者：　　小池文人（横浜国大），既分布の外来生物の分布拡大データは森本信生（畜産草地研究所），および昆虫情報処理研究会のゴケグモ類の情報センター，厚生労働省による過去の新型インフルエンザ情報（過去のまとめ検証用），環境省のヒアリに関する諸情報について，農林水産省のCSF感染野生イノシシの発見地点などによる．

　

文献：

Koike, F. and Morimoto, N. 2018. Supervised forecasting of the range expansion of novel non-indigenous organisms: alien pest organisms and the 2009 H1N1 flu pandemic. Global Ecology and Biogeography 27:991–1000. https://doi.org/10.1111/geb.12754

ホームへ